A álgebra, uma das áreas mais intrigantes e desafiadoras da matemática, tem sido uma ferramenta essencial para entender e descrever o mundo ao nosso redor desde tempos antigos. Seu papel se estende além das salas de aula, alcançando diversas áreas do conhecimento, como física, engenharia, economia e ciência da computação.
Mas o que é essa disciplina? Em termos amplos, é um ramo da matemática que estuda as propriedades das operações aritméticas e as relações entre elementos desconhecidos, representados por símbolos. Ao manipular esses símbolos e expressões, essa disciplina nos permite resolver problemas complexos e descobrir padrões subjacentes.
Neste artigo, vamos explorar mais profundamente o que é essa disciplina, seus fundamentos e suas aplicações práticas.
O que é essa disciplina?
Essa área da matemática estuda as estruturas algébricas, ou seja, conjuntos de elementos que podem ser combinados por meio de operações matemáticas. Portanto, ela permite representar situações abstratas ou generalizadas por meio de símbolos, letras e números, que formam as expressões algébricas.
Quais conteúdos envolvem essa disciplina?
Essa área da matemática abrange diversos conteúdos que são estudados ao longo da educação básica e superior. Alguns dos principais são:
Expressões algébricas
São combinações de números, letras e sinais de operações que representam uma quantidade ou uma relação matemática. Por exemplo: 2x + 3y – 5, a² + b² = c², x³ – 2x + 1.
Propriedades das operações matemáticas
São regras que valem para todas as operações matemáticas e que permitem simplificar ou resolver expressões algébricas. Por exemplo: a + b = b + a (comutativa da adição), a(b + c) = ab + ac (distributiva da multiplicação sobre a adição), (a + b)² = a² + 2ab + b² (quadrado da soma).
Conheça mais!
Equações
São expressões algébricas que contêm uma igualdade e uma ou mais incógnitas, que são as letras que representam valores desconhecidos. Sendo assim, o objetivo é encontrar o valor das incógnitas que tornam a igualdade verdadeira. Por exemplo: 2x – 3 = 5 (equação do primeiro grau), x² – 5x + 6 = 0 (equação do segundo grau), sen x = 0,5 (equação trigonométrica).
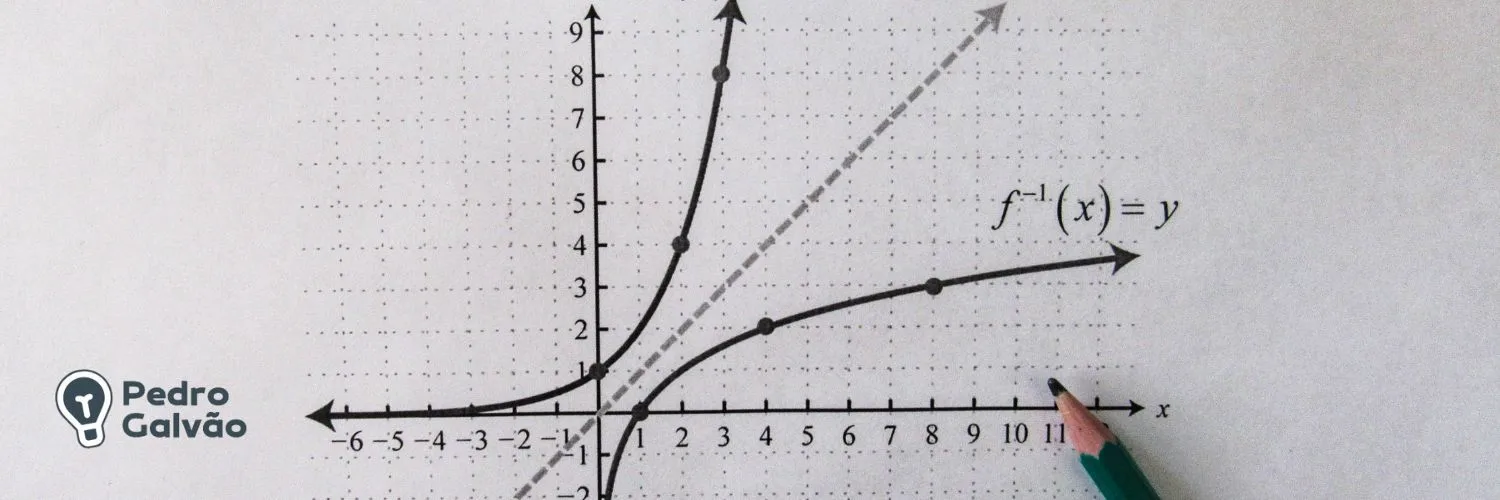
Funções
São relações entre dois conjuntos de elementos, chamados de domínio e imagem, que associa cada elemento do domínio a um único elemento da imagem. Por isso, as funções podem ser representadas por fórmulas algébricas, tabelas, gráficos ou palavras. Por exemplo: f(x) = 2x + 1 (função afim), f(x) = x² – 4 (função quadrática), f(x) = log x (função logarítmica).
Álgebra clássica e álgebra abstracta
A álgebra clássica é a parte da álgebra que estuda as estruturas algébricas mais simples e familiares, como os números reais, os números complexos, os polinômios, as matrizes e os determinantes.
A álgebra abstrata, por outro lado, é a parte da álgebra que estuda as estruturas algébricas mais gerais e abstratas, como os grupos, os anéis, os corpos e os espaços vetoriais.
Dicas para estudar essa disciplina
Algumas dicas para estudar essa disciplina são:
- Revisar os conceitos básicos de aritmética, como as operações fundamentais, as frações, os expoentes e as raízes.
- Praticar bastante a resolução de exercícios de diferentes níveis de dificuldade e tipos de problemas.
- Usar recursos visuais, como gráficos, tabelas e diagramas, para facilitar a compreensão das relações algébricas.
- Buscar aplicações práticas dessa disciplina em outras áreas do conhecimento, como física, química, biologia e economia.
- Recorrer a materiais complementares, como livros, vídeos, jogos e aplicativos, para reforçar o aprendizado.
- Entender essa disciplina é fundamental para o processo completo de aprendizagem da matemática. Espero que esse artigo tenha te ajudado a compreender melhor.
Perguntas frequentes sobre essa álgebra
A palavra álgebra vem do árabe al-jabr, que significa “reunião de partes quebradas”. Esse termo foi usado pelo matemático persa Al-Khwarizmi no título de seu livro Al-jabr wa’l-muqabala (“A reunião e a redução de termos”), que é considerado o primeiro tratado de álgebra.
Álgebra e geometria são dois ramos da matemática que se relacionam entre si, mas têm enfoques diferentes. A álgebra estuda as estruturas algébricas e as operações matemáticas, enquanto a geometria estuda as formas, as medidas e as posições dos objetos no espaço.
A álgebra é importante porque permite representar e resolver situações matemáticas de forma geral e abstrata, sem depender de valores específicos. Além disso, a álgebra é fundamental para o desenvolvimento de outras áreas da matemática, como o cálculo, a análise, a teoria dos números e a criptografia.